![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()


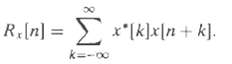

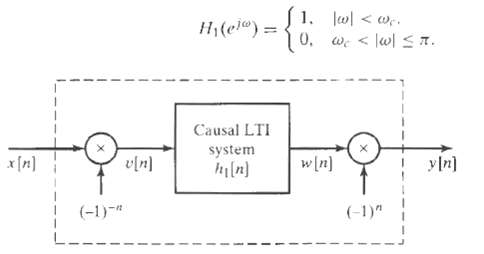
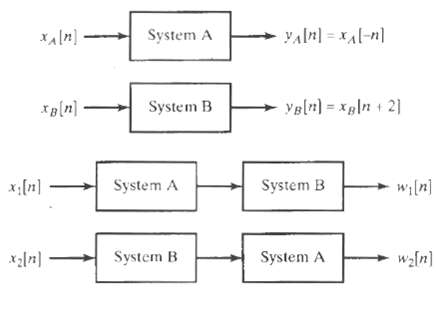
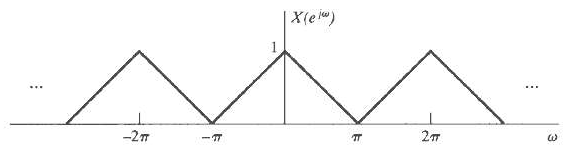
![yı[n] S1 y[n] x[n] S2 y2[n] Part b 0, unspecified, 0.27 < |w < x, |wl < 0.27, Hi(ei](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/8/8/9/3845c616f6833fba1549936310483.jpg)





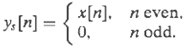
![x[n+ N]x*[n – N]e¬jom Ox{N, w) = %3D n=-00 (a) Show that Ox(-N. -w) = 0;(N, w). (b) If 0 < a < 1, x[n] = Aa](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1553/0/6/9/9635c91f78bb325e1553069964949.jpg)
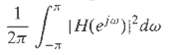
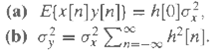
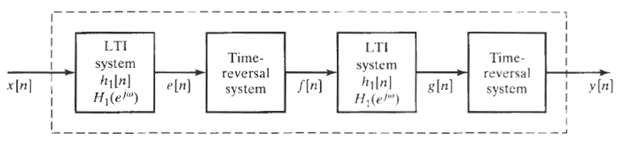
![hi[n} x [n] = o? £k-0 ha[n] y[n] w [n] |(a) Is o h{[k]? (b) Is o=D oΣkE0 h[시? uk:](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/9/4/7/9275c625417149b41549994853973.jpg)

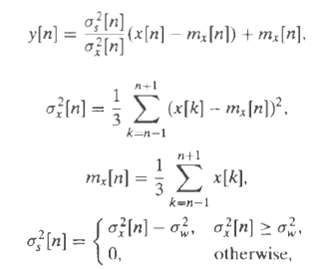
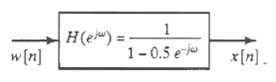
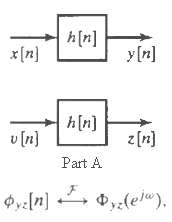
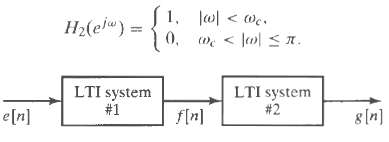
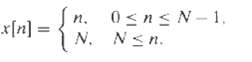
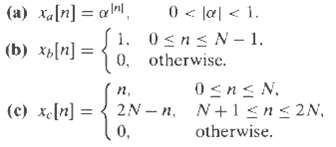


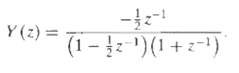
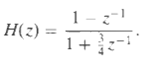
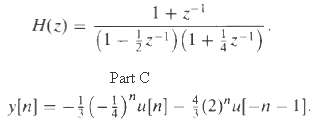
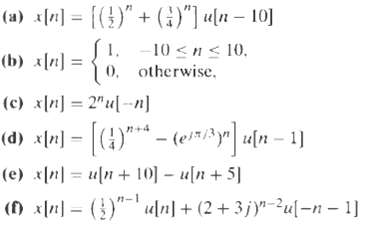
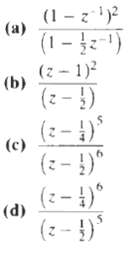

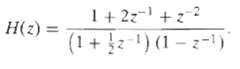
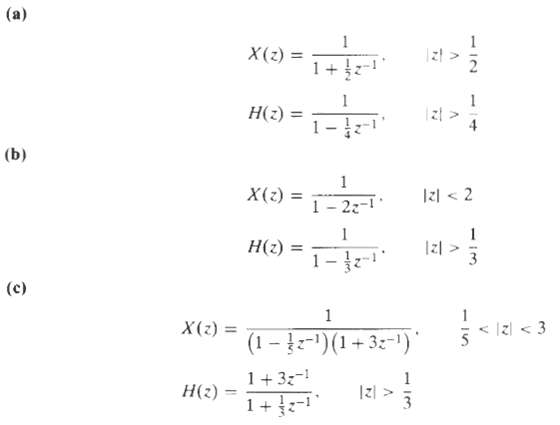
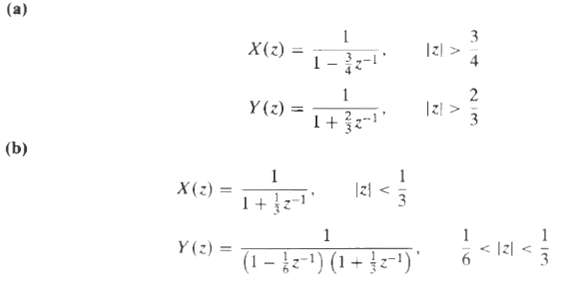
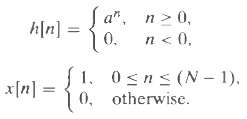
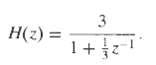
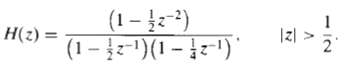
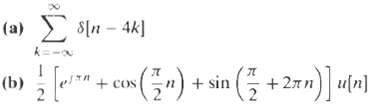
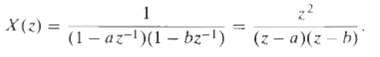

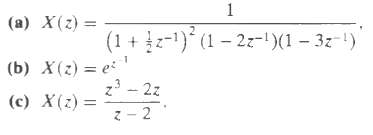


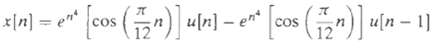
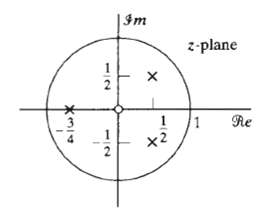

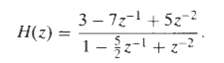
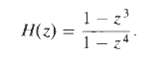
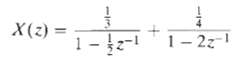
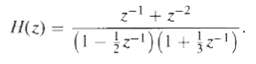
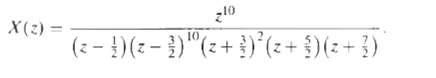
![e[n] Не) v[n] w[n} x[n]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/9/5/7/4085c627920acb8c1550004336067.jpg)
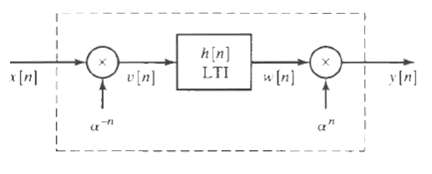
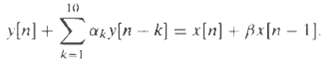

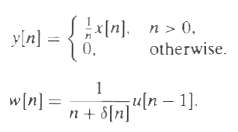
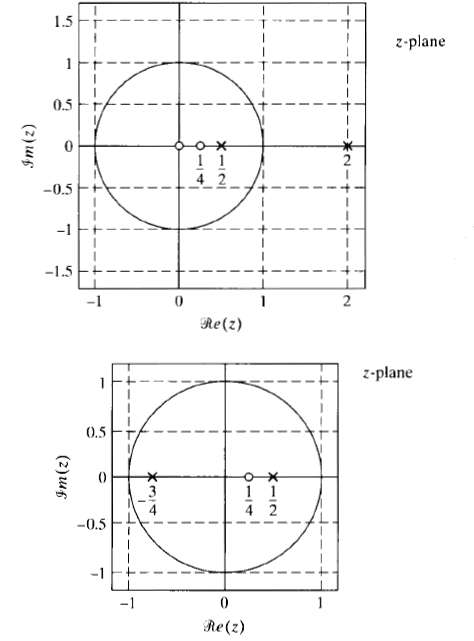
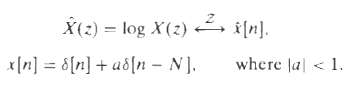
![|X(z) : v_2[u]x Z = (2)X n=-00](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/9/5/8/7785c627e7a697861550005705229.jpg)

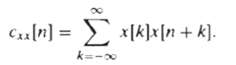


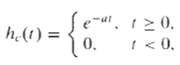

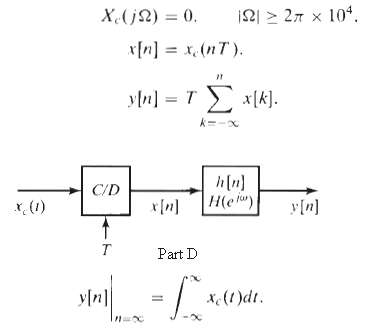
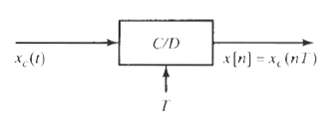
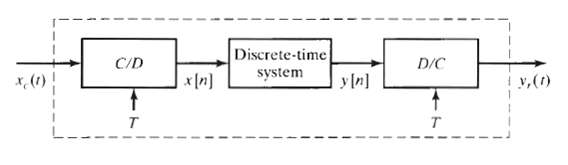
![C/D x.(1) x [n] = x,(nT)](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1549/9/6/5/7555c6299bbcb82d1550012681709.jpg)