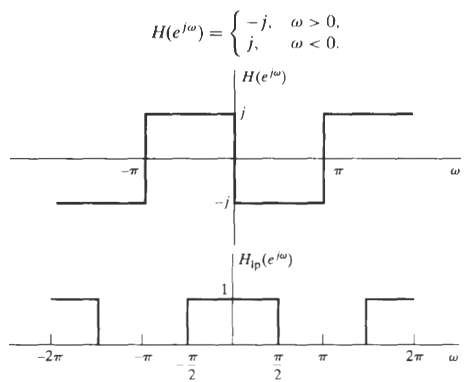
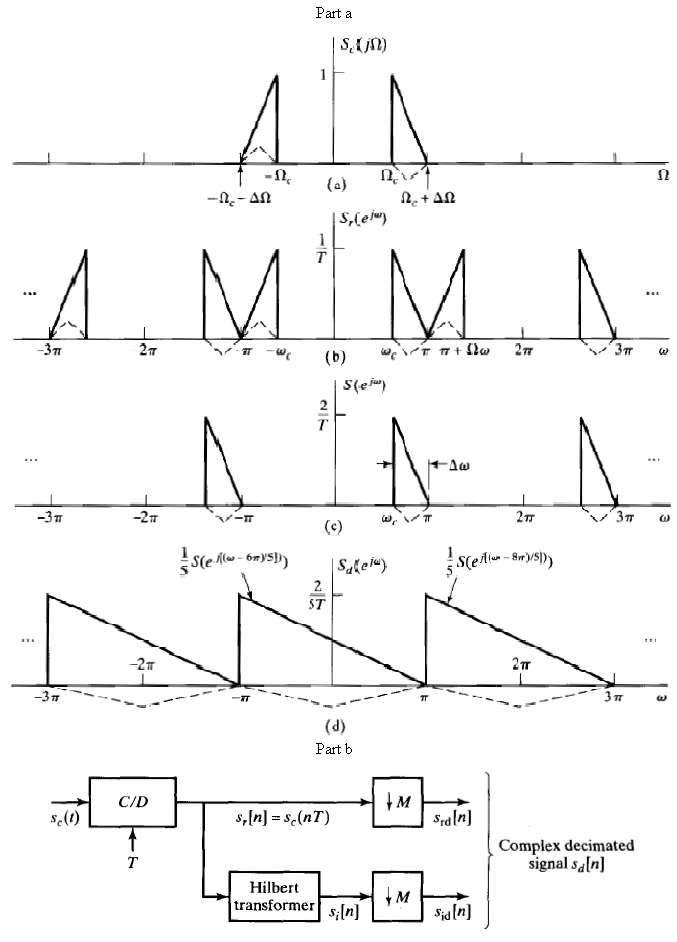
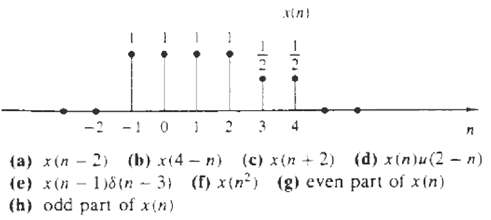
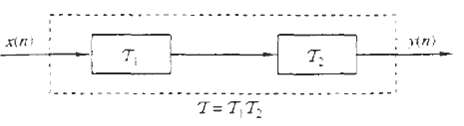
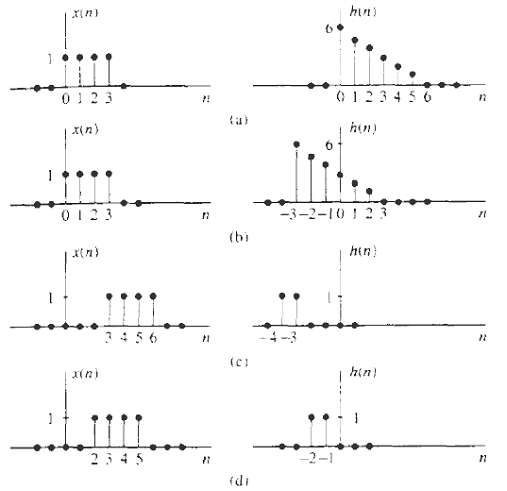
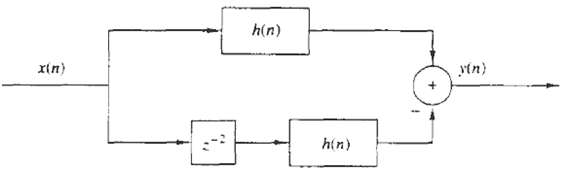
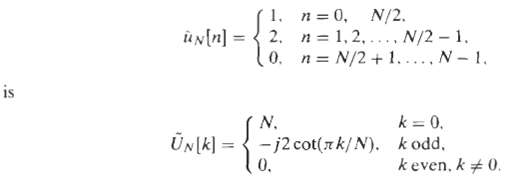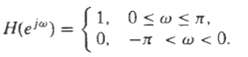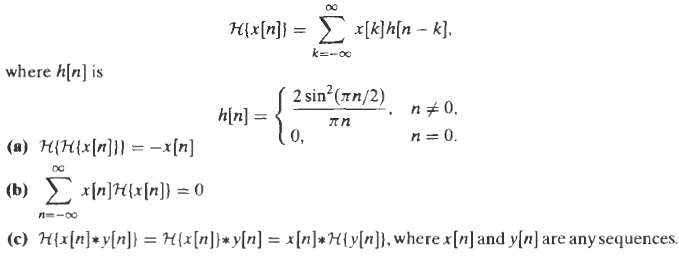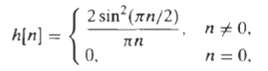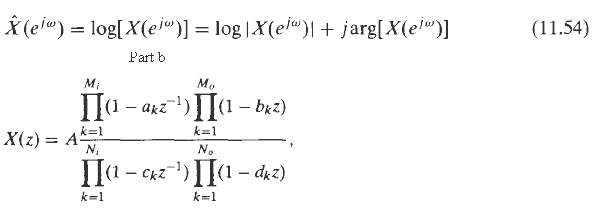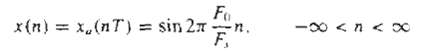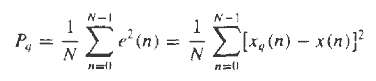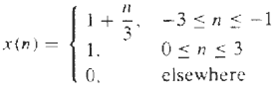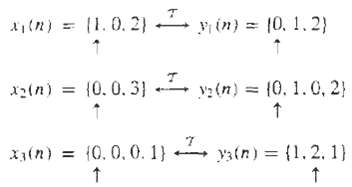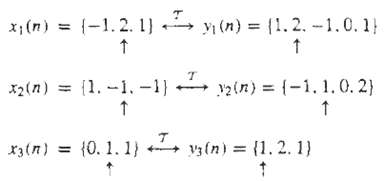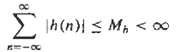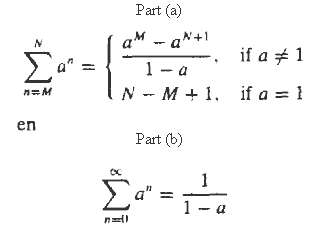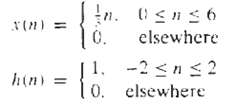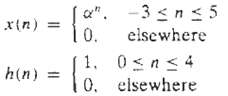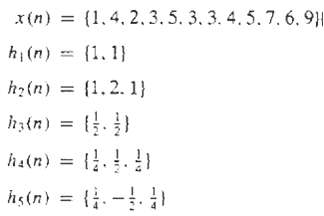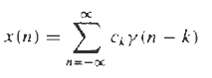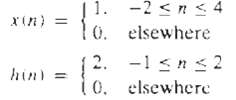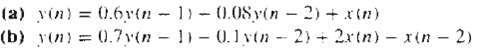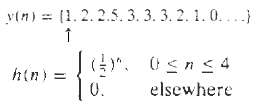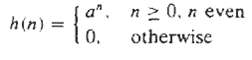Digital Signal Processing 3rd Edition Jonh G. Proakis, Dimitris G.Manolakis - Solutions
Discover comprehensive solutions and answers for "Digital Signal Processing 3rd Edition" by John G. Proakis and Dimitris G. Manolakis. Access an extensive collection of solved problems and step-by-step answers online, including an in-depth answers key and chapter solutions. Our solution manual, available in PDF format, provides detailed explanations and is an invaluable resource for students and instructors alike. Enhance your learning with our instructor manual and textbook resources, all available for free download. Whether you're studying for a test bank or seeking specific questions and answers, our expertly compiled guide offers everything you need to excel.
Get 50% OFF
Claim Now
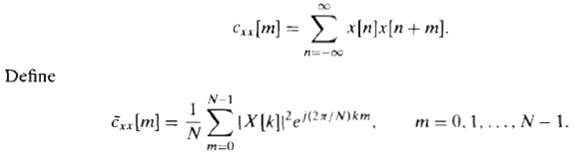
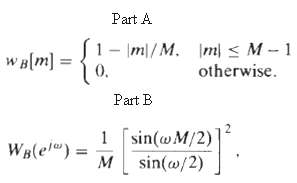
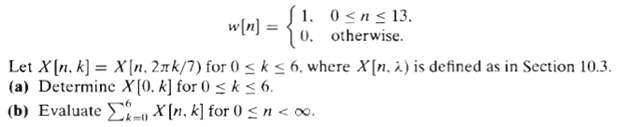
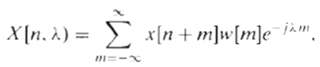
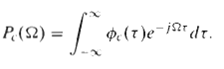
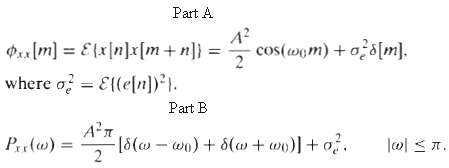
![Σh Н(): 1- акг* k=0 -Σαε. k=1 Уin - У акуп - к)+ bextn - k]. k=1 k=0 Part E Фу0] — акфуy[k] + о.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/1/6/0865c666b96083261550216085647.jpg)
![έξθ, x. (1) eiki 16 k=-4 Part B 16-point DFT C/D g[n} G(k] 2т u{n] – u[n - 16] 16](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/1/6/3015c666c6da1cb91550216301283.jpg)
![S x[n]. 0<n< 255, otherwise, 10. î[n] = î[n}: 0, Part C w = 0, w = ±2x/L, 0, w = 2nk/L. 1. Warg (eiu) a, for k = 2, 3](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/1/6/4815c666d21e4dac1550216481555.jpg)
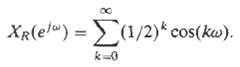
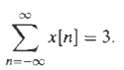
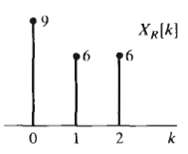
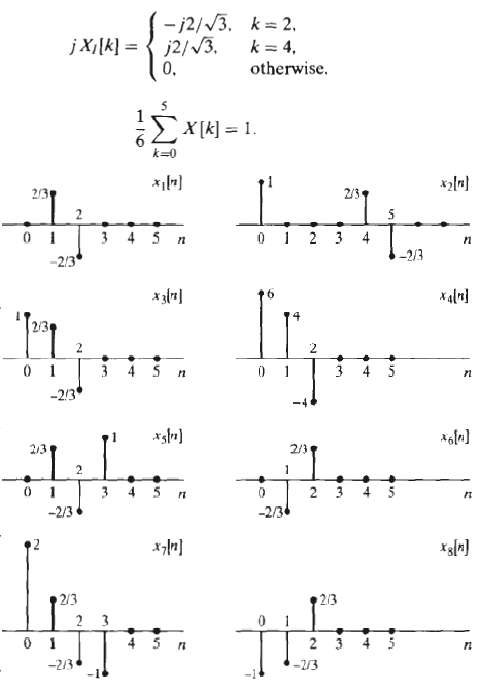
![X(3)-Σ[a]ες. x[n]z¯ п-о Part a (1) av au au av ду](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/2/3/7005c66895471a0b1550223700023.jpg)
