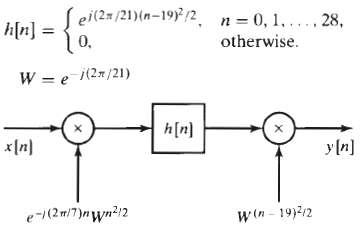
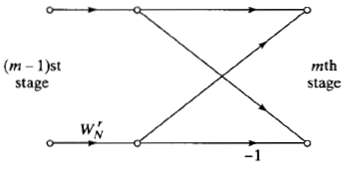
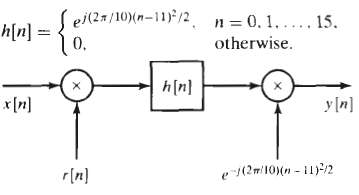
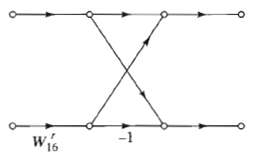
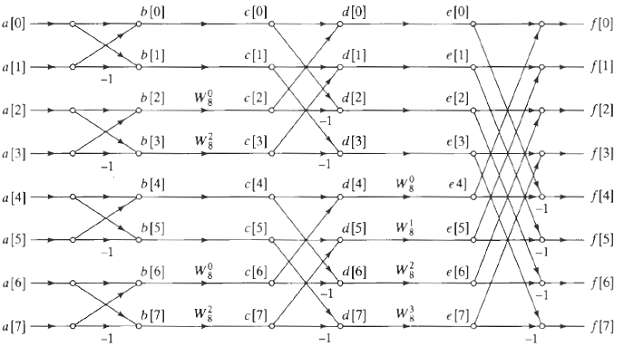
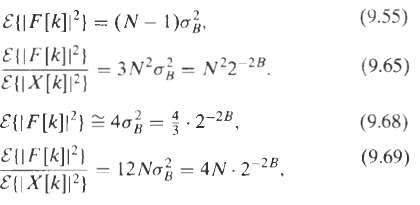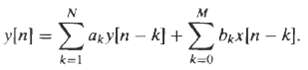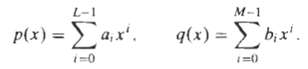![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()





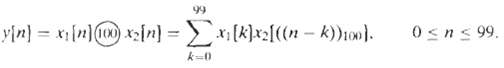
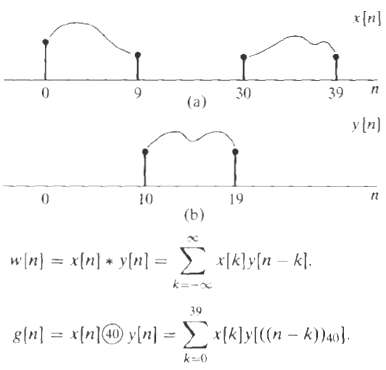
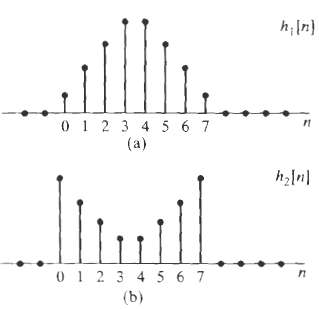
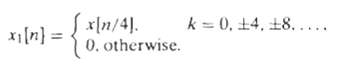
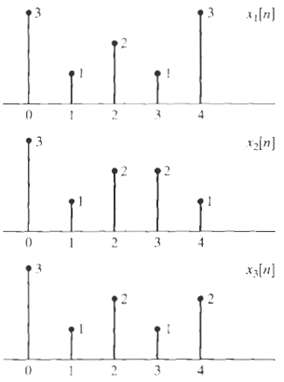
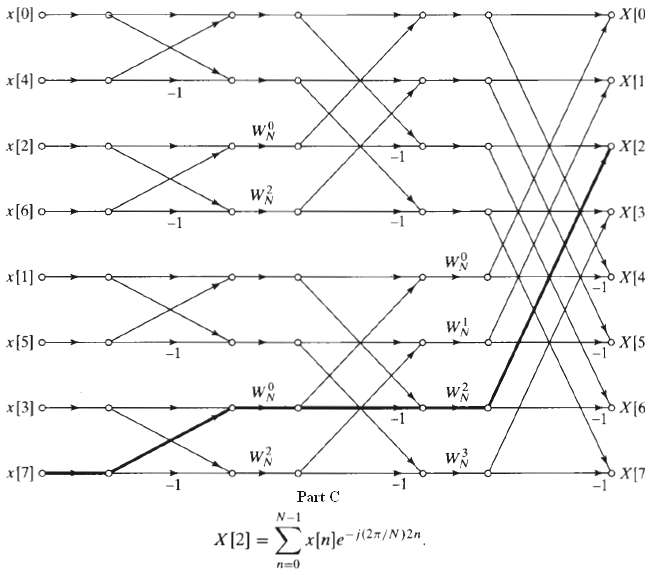
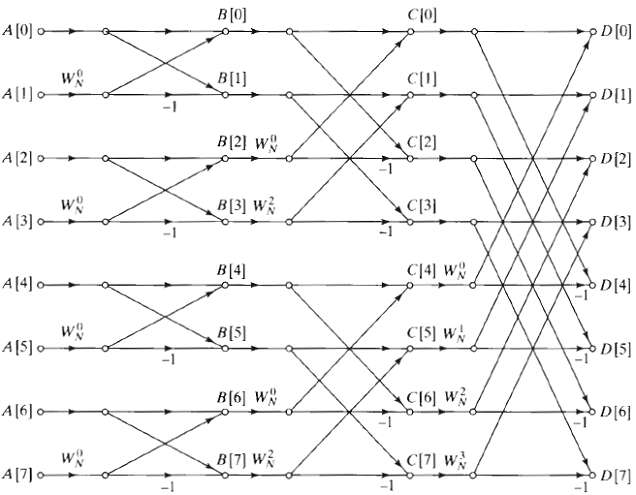
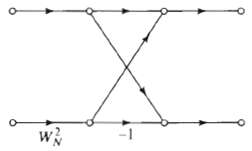
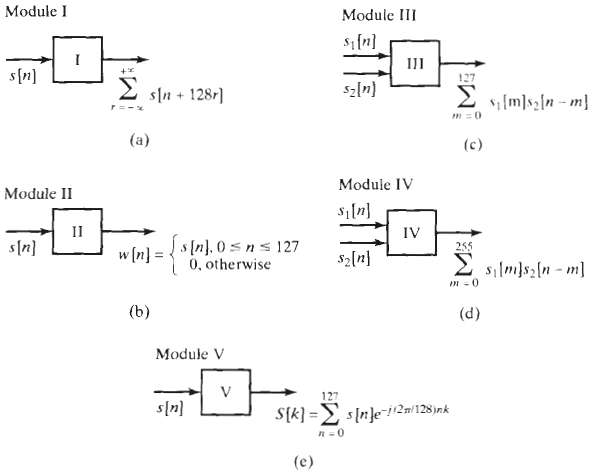
![Part A X|k]e(2a/8)kn t%39 Part D S 2X(k]. k = 0, 2, 4. 6. k = 1. 3, 5, 7. 0. Y(k]](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/0/5/7975c664365949251550205797337.jpg)
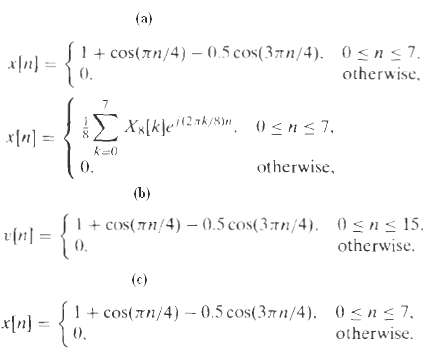


![Periodic Sequence (Period N) DFS Cocfficients (Period N) *(k] 10. *|-n) X.k] = }(X(k] + **(-k) X,k] = }(X[k] – X*l-k](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/0/6/9505c6647e6a5d111550206949557.jpg)
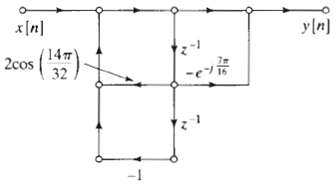
![š[n]. 0<n< N – 1, otherwise. 0, x[n] = (8.57) N-1 E x[m] E WN E x(m]p[n – m]. ř[n] = (8.54) k=0 m=-00 m=-0 sin[(wN](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/0/7/0815c6648693a2ee1550207080966.jpg)

![V[k] = (W – bW)Y[R]. N.](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/0/7/6945c664ace550151550207693062.jpg)
![X 4[k] = X(z)| k = 0, 1. 2. .... N – 1. z=e{?+k;Ni+;N](https://dsd5zvtm8ll6.cloudfront.net/si.question.images/images/question_images/1550/2/0/7/7745c664b1ecda861550207774578.jpg)