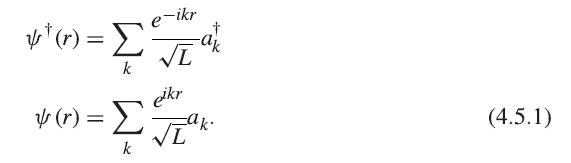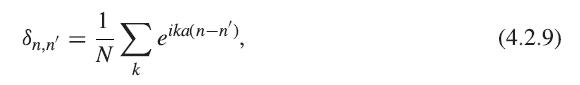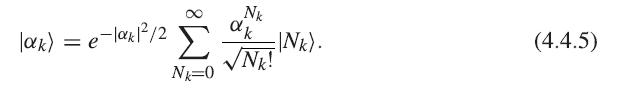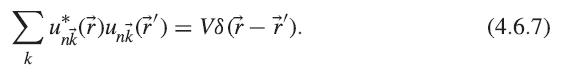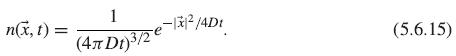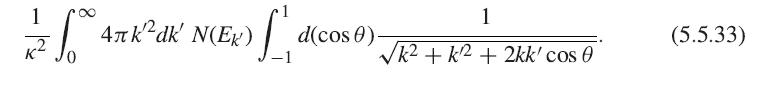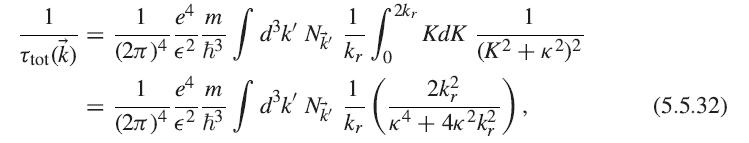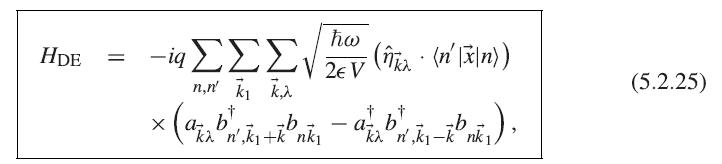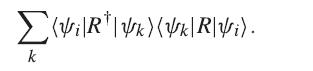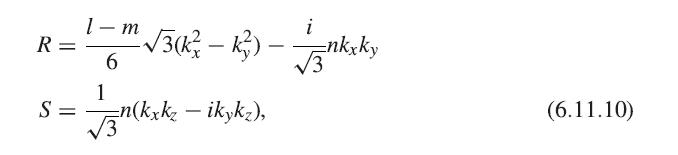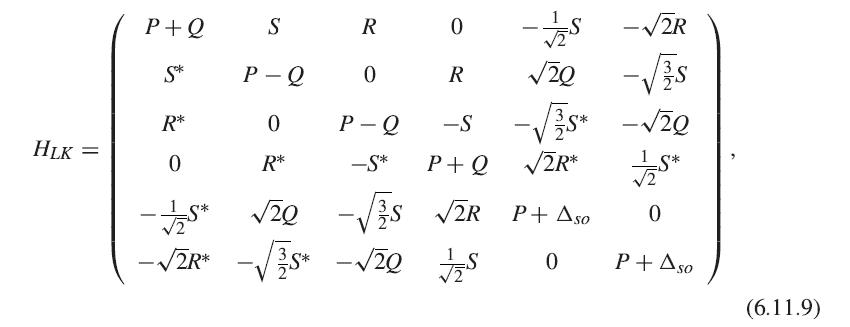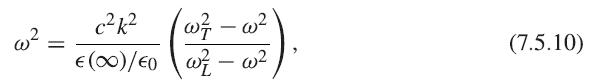Solid State Physics Essential Concepts 2nd Edition David W. Snoke - Solutions
Discover a comprehensive resource for "Solid State Physics Essential Concepts 2nd Edition" by David W. Snoke. Access online answers key and in-depth solutions with our exclusive solution manual and solutions PDF. Delve into solved problems and explore questions and answers with our test bank and chapter solutions. Benefit from step-by-step answers, crafted for clarity, in our instructor manual tailored for this textbook. Whether you're studying or teaching, enjoy the convenience of a free download, offering clear guidance and support for solid state physics studies. Unlock the potential of your learning journey today!
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()