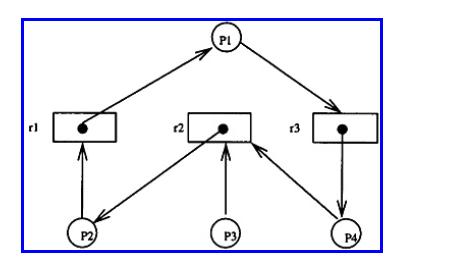
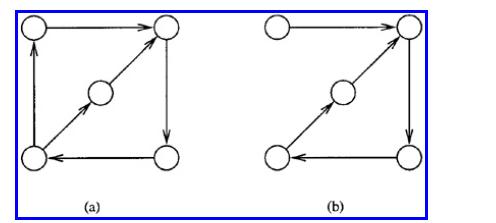
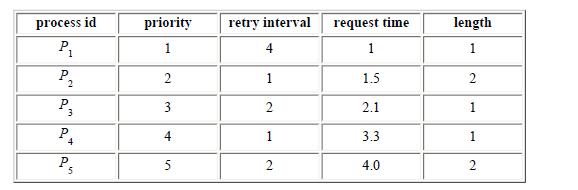
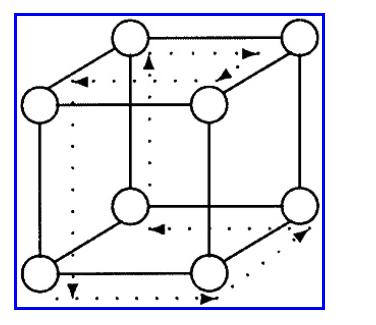
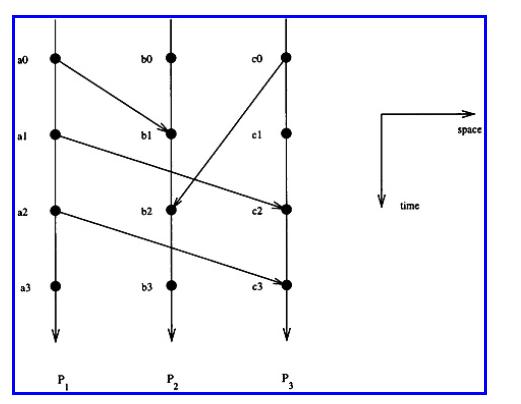
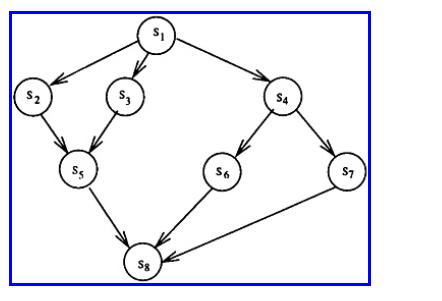
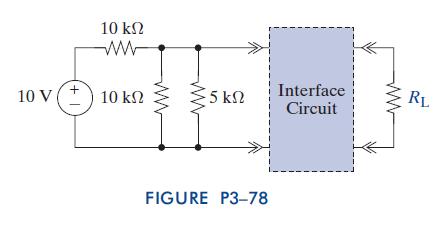
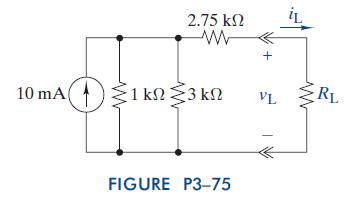
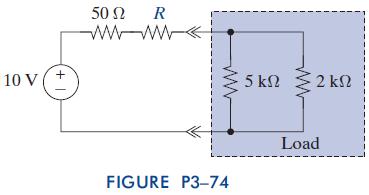
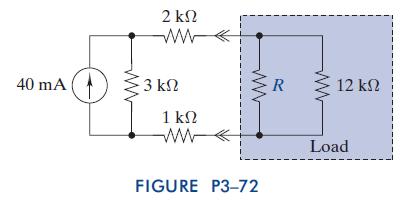
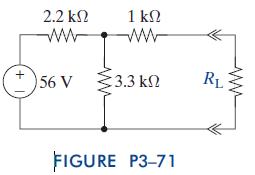
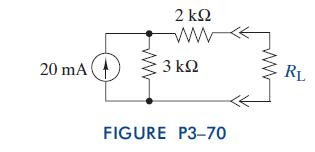
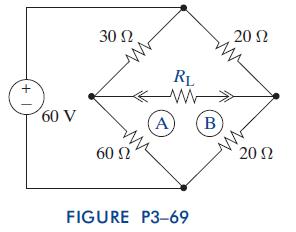
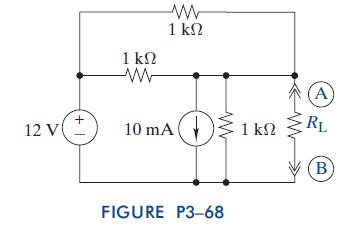
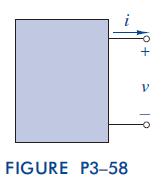
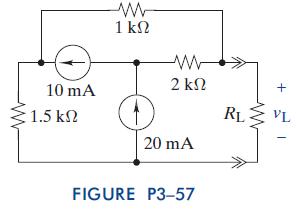
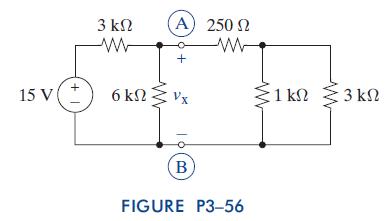
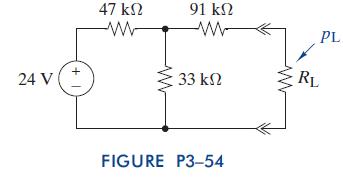
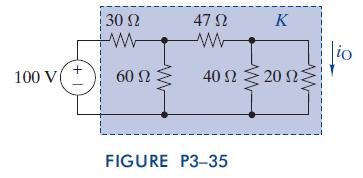
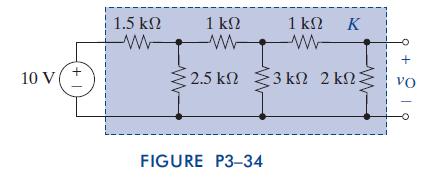
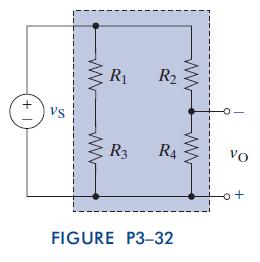
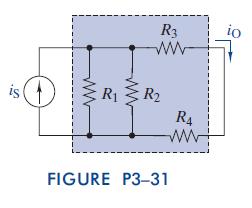
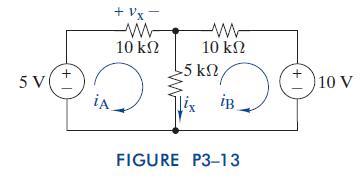
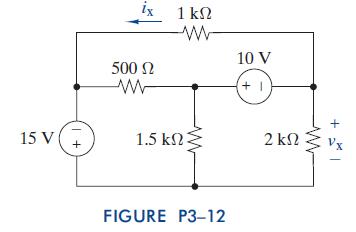
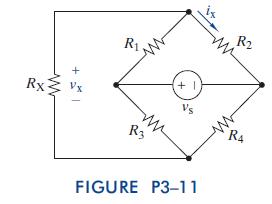
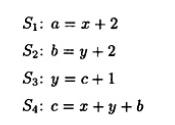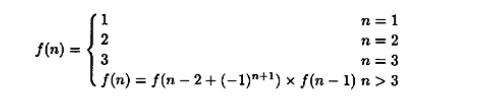The Analysis And Design Of Linear Circuits 7th Edition Roland E Thomas, Albert J Rosa, Gregory J Toussaint - Solutions
Unlock a world of knowledge with "The Analysis And Design Of Linear Circuits 7th Edition" by Roland E Thomas, Albert J Rosa, and Gregory J Toussaint. Dive into expertly crafted solutions with our comprehensive online answers key and solutions PDF. Explore step-by-step answers for each chapter, providing in-depth insights and solved problems for enhanced learning. Our solution manual and test bank offer an instructor's perspective, making it an invaluable resource for students and educators alike. Access the textbook's chapter solutions and questions and answers to refine your understanding. Enjoy the convenience of free download options to aid your academic journey.
![]()
![]() New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
New Semester Started
Get 50% OFF
Study Help!
--h --m --s
Claim Now
![]()
![]()