New Semester
Started
Get
50% OFF
Study Help!
--h --m --s
Claim Now
Question Answers
Textbooks
Find textbooks, questions and answers
Oops, something went wrong!
Change your search query and then try again
S
Books
FREE
Study Help
Expert Questions
Accounting
General Management
Mathematics
Finance
Organizational Behaviour
Law
Physics
Operating System
Management Leadership
Sociology
Programming
Marketing
Database
Computer Network
Economics
Textbooks Solutions
Accounting
Managerial Accounting
Management Leadership
Cost Accounting
Statistics
Business Law
Corporate Finance
Finance
Economics
Auditing
Tutors
Online Tutors
Find a Tutor
Hire a Tutor
Become a Tutor
AI Tutor
AI Study Planner
NEW
Sell Books
Search
Search
Sign In
Register
study help
physics
modern classical physics
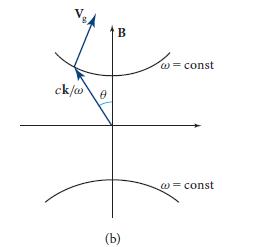
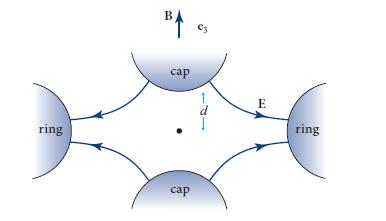
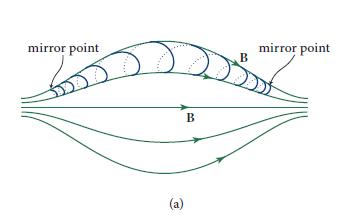
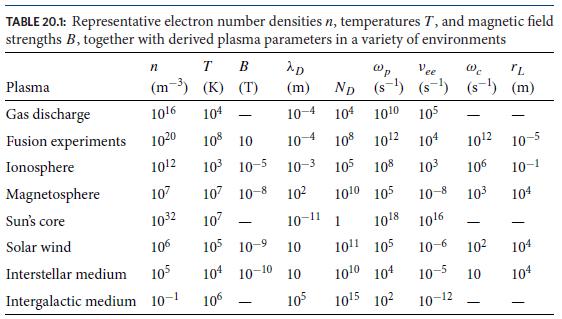
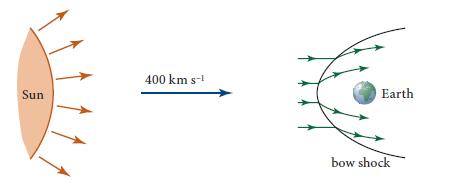
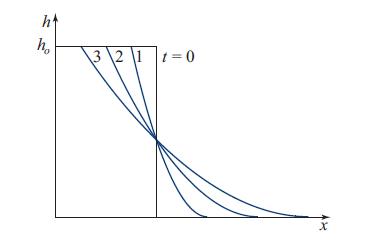
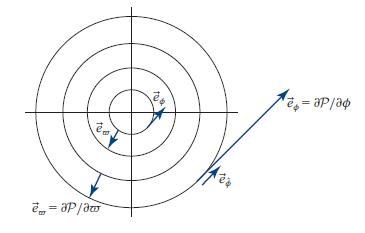
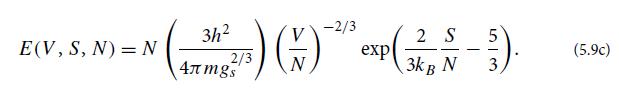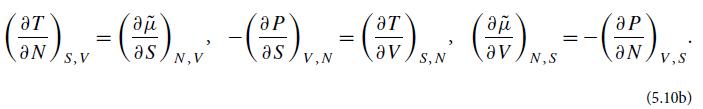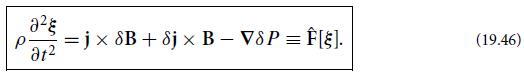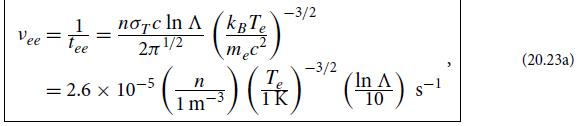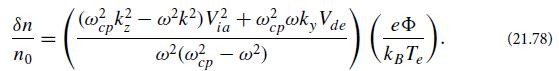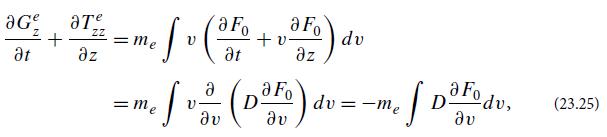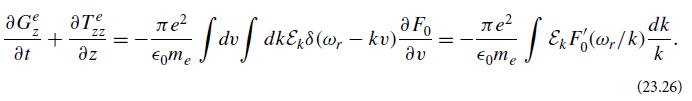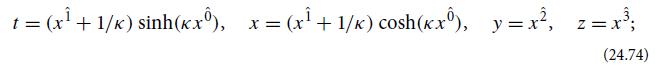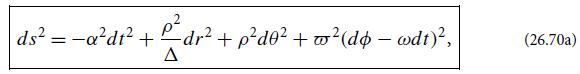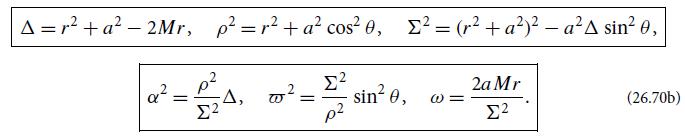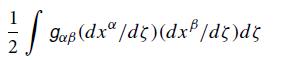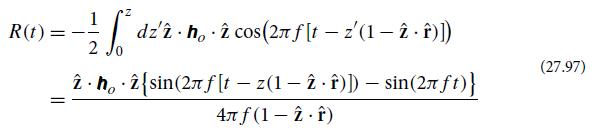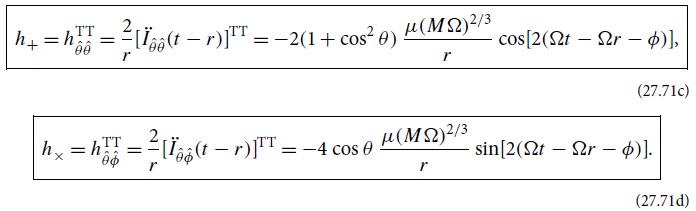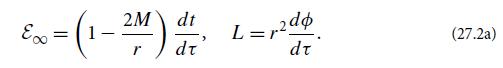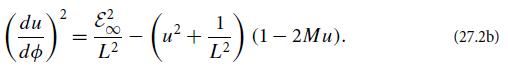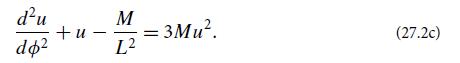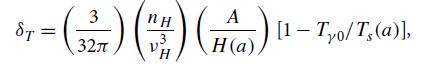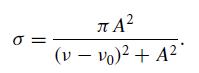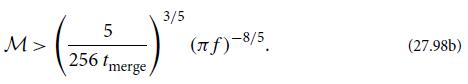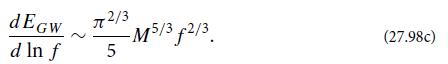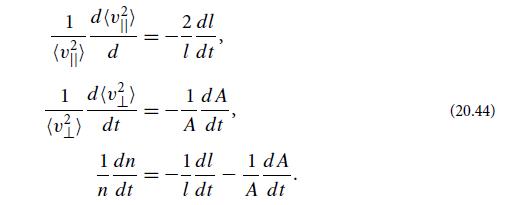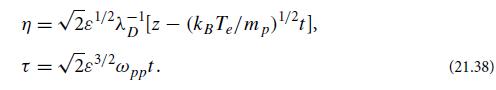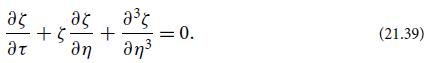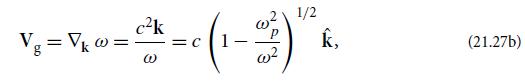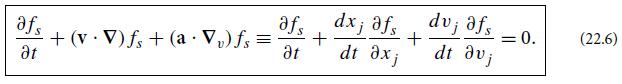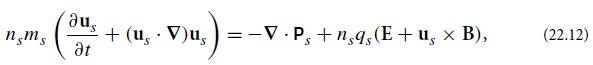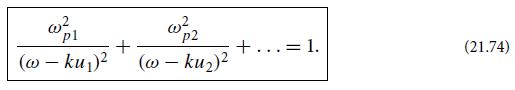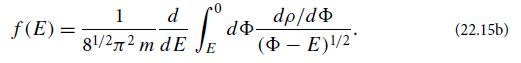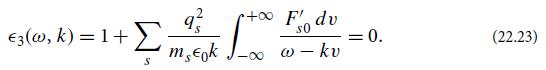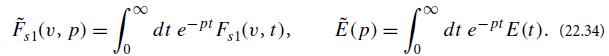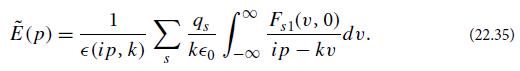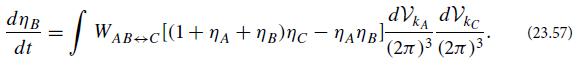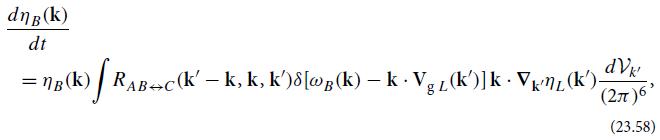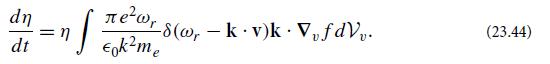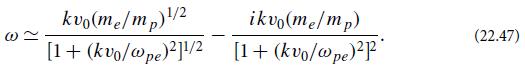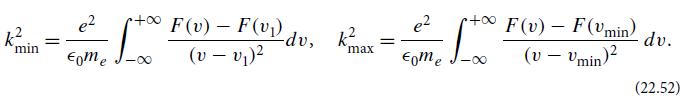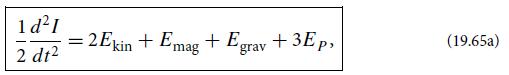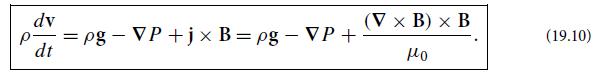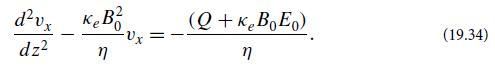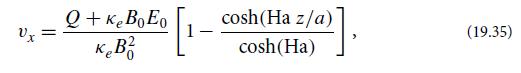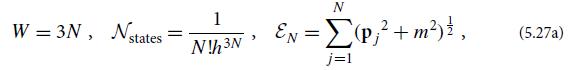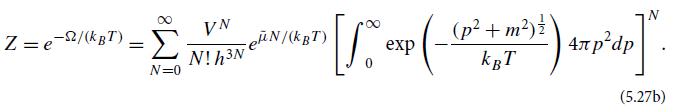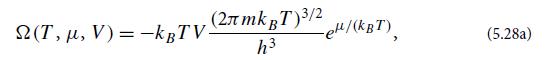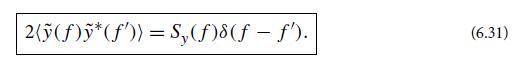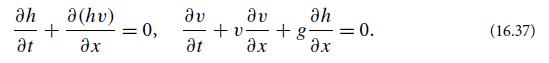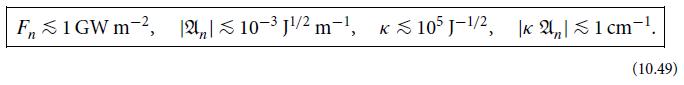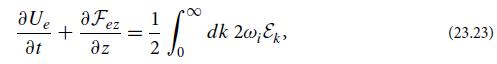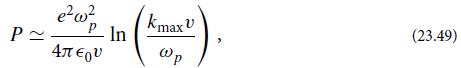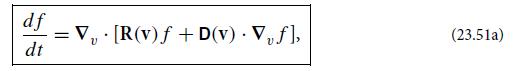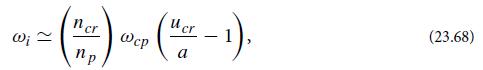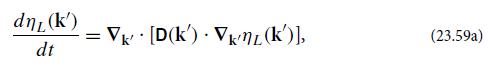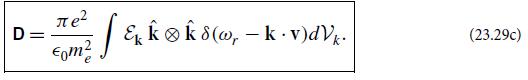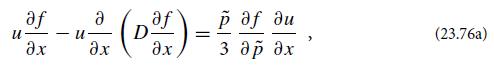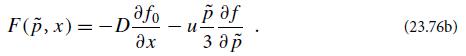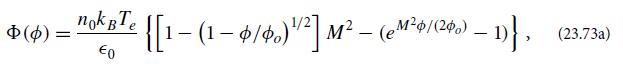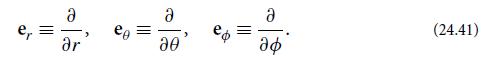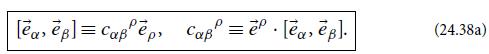Modern Classical Physics Optics Fluids Plasmas Elasticity Relativity And Statistical Physics 1st Edition Kip S. Thorne, Roger D. Blandford - Solutions
Another interesting 1-dimensional map is provided by the recursion relation(a) Consider the asymptotic behavior of the variable xn for different values of the parameter a, with both xn and a being confined to the interval [0, 1]. In particular, find that for 0 crit (for some acrit), the sequence xn
One of the first discoveries of chaos in a mathematical model was by Lorenz (1963), who made a simple model of atmospheric convection. In this model, the temperature and velocity field are characterized by three variables, x, y, and z, which satisfy the coupled, nonlinear differential equations(The
To measure a very weak sinusoidal force, let the force act on a simple harmonic oscillator with eigenfrequency at or near the force’s frequency, and measure the oscillator’s response. Examples range in physical scale from nanomechanical oscillators (∼1μm in size) with eigenfrequency ∼1GHz
Consider a cell with volume V , like those of Fig. 5.1, that has imaginary walls and is immersed in a bath of identical, nonrelativistic, classical perfect-gas particles with temperature Tb and chemical potential μb. Suppose that we make a large number of measurements of the number of particles in
Water and its vapor (liquid and gaseous H2O) can be described moderately well by the van der Waals model, with the parameters a = 1.52 × 10−48J m3 and b = 5.05 × 10−29m3 determined by fitting to the measured pressure and temperature at the critical point (inflection point C in Fig. 5.8a: Pc =
Exercise 5.5 explored the enthalpy representation of thermodynamics for an equilibrium ensemble of systems in contact with a volume bath. Here we extend that analysis to an ensemble out of equilibrium. We denote by Pb the bath pressure.(a) The systems exchange volume but not heat or particles with
Consider a gigantic container of gas made of identical particles that might or might not interact. Regard this gas as a bath, with temperature Tb and pressure Pb. Pick out at random a sample of the bath’s gas containing precisely N particles, with N >> 1. Measure the volume V of the sample
Consider an optically thick hydrogen gas in statistical equilibrium at temperature T. (“Optically thick” means that photons can travel only a small distance compared to the size of the system before being absorbed, so they are confined by the hydrogen and kept in statistical equilibrium with
Random processes can be stochastic functions of some variable or variables other than time. For example, it is conventional to describe fractional fluctuations in the largescale distribution of mass in the universe, or the distribution of galaxies, using the quantity(not to be confused with the
Prove Doob’s theorem. More specifically, for any Gaussian-Markov random process, show that P2(y2, t|y1) is given by Eqs. (6.18a,b).(a) Show that the Gaussian process ynew has probability distributionsand show that the constant C21 that appears here is the correlation function C21 = Cy(t2 −
Suppose that you have a noisy receiver of weak signals (e.g., a communications receiver). You are expecting a signal s(t) with finite duration and known form to come in, beginning at a predetermined time t = 0, but you are not sure whether it is present. If it is present, then your receiver’s
(a) Write down the partition function for a 1-dimensional Ising lattice as a sum over terms describing all possible spin organizations.(b) Show that by separating into even and odd numbered spins, it is possible to factor the partition function and relate z(N, K)exactly to z(N/2, K'). Specifically,
(a) If y is a random process with spectral density Sy(f), and w(t) is the output of the finite-Fourier-transform filter (6.58a), what is Sw(f)?(b) Sketch the filter function |K̃(f)2 for this finite-Fourier-transform filter, and show that its bandwidth is given by Eq. (6.58b).(c) An “averaging
Highly stable clocks (e.g., cesium clocks, hydrogen maser clocks, or quartz crystal oscillators) have angular frequencies ω of ticking that tend to wander so much over very long timescales that their variances diverge. For example, a cesium clock has random-walk noise on very long timescales (low
(a) Explain why, physically, when the Brownian motion of a particle (which starts at x = 0 at time t = 0) is observed only on timescales △τ >> τr corresponding to frequencies f r , its position x(t)must be a Gaussian-Markov process with x̄ = 0.What are the spectral density of x(t) and
Estimate how long it would take a personal computer to calculate the partition function for a 32 × 32 Ising lattice by evaluating every possible state.
(a) Show that the kernels K(τ) in Eq. (6.47) produce the indicated outputs w(t). Deduce the ratio Sw(f)/Sy(f ) =|K̃(f)|2 in two ways: (i) By Fourier transforming each K(τ); (ii) By setting y = ei2πft , deducing the corresponding filtered output w directly from the expression for w in terms of
(a) Show that for shot noise, y(t) = ∑i F(t − ti), the spectral density Sy(f ) is given by Eq. (6.68b). Show that the relaxation time appearing in the correlation function is approximately the duration τp of F(t).(b) Suppose the shapes of Fj (t − tj) are all different instead of being
Let u and ν be two random processes. Show thatwhere R denotes the real part of the argument. Su+v(f) = Su(f) + S₂(f) + Suv (f) + Svu (f) = Su(f) + S, (f)+2RSuv (f), (6.43)
(a) Show that for shot noise with identical pulses that have the infinitely sharply peaked shape of Eq. (6.45), the power spectrum has the flicker form Sy ∝ 1/f for all f .(b) Construct realizations of shot noise with flicker spectrum[Eq. (6.68a) with pulse shape (6.45)] that range from a few
Consider an L-C-R circuit as shown in Fig. 6.15. This circuit is governed by the differential equation (6.72), where F´ is the fluctuating voltage produced by the resistor’s microscopic degrees of freedom (so we shall rename it V´), and F ≡ V vanishes, since there is no driving voltage in the
By a method analogous to that used for the elementary fluctuation-dissipation theorem, derive the generalized fluctuation-dissipation theorem [Eqs. (6.86)].Consider a thought experiment in which the system’s generalized coordinate q is very weakly coupled to an external oscillator that has a mass
Derive Eqs. (6.96) for A and B from the Fokker-Planck equation (6.94), and then from Eqs. (6.96) derive Eqs. (6.97).Equations Ә - P2 Ət = Ә ду -[A(y)Pz] + 1 02 2 ду2 -[B(y) P2]. (6.94)
(a) Write down the explicit form of the Langevin equation for the x component of velocity v(t) of a dust particle interacting with thermalized air molecules.(b) Suppose that the dust particle has velocity v at time t. By integrating the Langevin equation, show that its velocity at time t + △t is
Consider an electron that can transition between two levels by emitting or absorbing a photon; and recall that we have argued that the stimulated transitions should be microscopically reversible. This is an example of a general principle introduced by Boltzmann called detailed balance. In the
Consider a classical simple harmonic oscillator (e.g., the nanomechanical oscillator, LIGO mass on an optical spring, L-C-R circuit, or optical resonator briefly discussed in Ex. 6.17). Let the oscillator be coupled weakly to a dissipative heat bath with temperature T . The Langevin equation for
Show that the Fokker-Planck equation can be interpreted as a conservation law for probability. What is the probability flux in this conservation law? What is the interpretation of each of its two terms?
Derive the group and phase velocities (7.10)–(7.13) from the dispersion relations (7.4)–(7.7). w = 22 (k)=Ck = C|k], (7.4)
(a) Show that the prototypical scalar wave equation (7.17) follows from the variational principlewhere L is the lagrangian density(b) For any scalar-field lagrangian density L(ψ, ∂ψ/∂t , ∇ψ, x, t), the energy density and energy flux can be expressed in terms of the lagrangian, in Cartesian
(a) In connection with Eq. (7.35b), explain whyis the tiny volume occupied by a collection of the wave’s quanta.(b) Choose for the collection of quanta those that occupy a cross sectional area A orthogonal to a chosen ray, and a longitudinal length △s along the ray, so V = A△s. Show that d ln
Consider a 1-dimensionalwave packetwith dispersion relation ω = Ω(k). For concreteness, let A(k)be a narrow Gaussian peaked around(a) Expand α as α(k) = αo − xoκ with xo a constant, and assume for simplicity that higher order terms are negligible. Similarly, expand ω ≡ Ω(k) to quadratic
Consider the nonrelativistic Schrödinger equation for a particle moving in a time dependent, 3-dimensional potential well:(a) Seek a geometric-optics solution to this equation with the form ψ = AeiS/ℏ, where A and V are assumed to vary on a length scale L and timescale T long compared to
Consider two spherical mirrors, each with radius of curvature R, separated by distance d so as to form an optical cavity (Fig. 7.9). A laser beam bounces back and forth between the two mirrors. The center of the beam travels along a geometric-optics ray.(a) Show, using matrix methods, that the
(a) Work through the derivation of Eq. (7.73) for the scaled time delay in the vicinity of the cusp caustic for our simple example [Eq. (7.68)], with the aid of a suitable change of variables.(b) Sketch the nesting of the contours for the elliptic umbilic catastrophe as shown for the other four
Show that Hamilton’s equations for the standard dispersionless dispersion relation (7.4) imply the same ray equation (7.48) as we derived using Fermat’s principle. w=2(k)=Ck = C[k], (7.4)
Derive the quasi-spherical solution (7.42) of the vacuum scalar wave equation −∂2ψ/∂t2 + ∇2ψ = 0 from the geometric-optics laws by the procedure sketched in the text. 4 B(Ct-r,0,0)i(Ct-r,0,0), r (7.42)
Consider a simple refracting telescope (Fig. 7.7) that comprises two converging lenses, the objective and the eyepiece. This telescope takes parallel rays of light from distant stars, which make an angle θ ≪ 1with the optic axis, and converts them into parallel rays making a much larger angle
Consider sound waves propagating in an atmosphere with a horizontal wind. Assume that the sound speed C, as measured in the air’s local rest frame, is constant. Let the wind velocity u = uxex increase linearly with height z above the ground: ux = Sz, where S is the constant shearing rate.
A microscope takes light rays from a point on a microscopic object, very near the optic axis, and transforms them into parallel light rays that will be focused by a human eye’s lens onto the eye’s retina (Fig. 7.8). Use matrix methods to explore the operation of such a microscope. A single lens
A particle travels in 1 dimension, along the y axis, making a sequence of steps △yj (labeled by the integer j ), each of which is △yj = +1 with probability 1/2, or △yj = −1with probability 1/2.(a) After N >> 1 steps, the particle has reached location What does the central limit
Modify your computer program from Ex. 5.17 to deal with the 2-dimensional Ising model augmented by an externally imposed, uniform magnetic field [Eqs. (5.80)]. Compute the magnetization and the magnetic susceptibility for wisely selected values of moB/J and K = J/(kBT ).Data from Exercises
Explain why, for any (stationary) random process,Use the ergodic hypothesis to argue thatThereby conclude that, for a Markov process, all the probability distributions are determined by the conditional probability P2(y2, t|y1). Give an algorithm for computing them. lim P₂(y2, tly₁) = 8(y₂ -
Write a simple computer program to compute the energy and the specific heat of a 2-dimensional Ising lattice as described in the text. Examine the accuracy of your answers by varying the size of the lattice and the number of states sampled.
Figure 8.17 depicts a two-lens system for spatial filtering (also sometimes called a “4f system,” since it involves five special planes separated by four intervals with lengths equal to the common focal length f of the two lenses). Develop a description, patterned after Abbes, of image
In LIGO and other GW interferometers, one potential source of noise is scattered light. When the Gaussian beam in one of LIGO’s cavities reflects off a mirror, a small portion of the light gets scattered toward the walls of the cavity’s vacuum tube. Some of this scattered light can reflect or
Our discussion of microlensing assumed a single star and a circularly symmetric potential about it. This is usually a good approximation for stars in our galaxy. However, when the star is in another galaxy and the source is a background quasar (Figs. 7.19, 7.20), it is necessary to include the
(a) Calculate the 1-dimensional Fourier transforms [Eq. (8.11a) reduced to 1 dimension] of the functions f1(x) ≡ e−x2/2σ2, and f2 ≡ 0 for x 2 ≡ e−x/h for x ≥ 0.(b) Take the inverse transforms of your answers to part (a) and recover the original functions.(c) Convolve the exponential
Use the parallel-transport law (7.103) to derive the relation (7.104). df ds -k (f dk ds (7.103)
An alternative derivation of the lens equation for a point-mass lens, Eq. (7.88), evaluates the time delay along a path from the source to the observer and finds the true ray by extremizing it with respect to variations of θ.(a) Show that the geometric time delay is given by(b) Next show that the
A Martian Rover is equipped with a single gyroscope that is free to pivot about the direction perpendicular to the plane containing its wheels. To climb a steep hill on Mars without straining its motor, it must circle the summit in a decreasing spiral trajectory. Explain why there will be an error
The van der Waals equation of state (P + a/v2)(v − b) = kBT for H2O relates the pressure P and specific volume (volume per molecule) v to the temperature T ; see Sec. 5.7. Figure 5.8 makes it clear that, at some temperatures T and pressures P, there are three allowed volumes v(T , P), one
Consider a cusp catastrophe created by a screen as in the example and described by a standard cusp potential, Eq. (7.73). Suppose that a detector lies between the folds, so that there are three images of a single point source with state variables ãi.(a) Explain how, in principle, it is possible
Consider an elliptical gravitational lens where the potential Ψ is modeled byDetermine the generic form of the caustic surfaces, the types of catastrophe encountered, and the change in the number of images formed when a point source crosses these surfaces. Note that it is in the spirit of
Suppose that a large black hole forms two images of a background source separated by an angle θ. Let the fluxes of the two images be F+ and F− < F+. Show that the flux from the source would be F+ − F− if there were no lens and that the black hole should be located an angular distance [1+
As we have emphasized, representing light using wavefronts is complementary to treating it in terms of rays. Sketch the evolution of the wavefronts after they propagate through a phase-changing screen and eventually form caustics. Do this for a 2-dimensional cusp, and then consider the formation of
Consider a self-focusing optical fiber discussed in Ex. 7.8, in which the refractive index iswhere r = |x|.(a) Write down the Helmholtz equation in cylindrical polar coordinates and seek an axisymmetric mode for which ψ = R(r)Z(z), where R and Z are functions to be determined, and z measures
(a) Suppose that you have two thin sheets with transmission functions t = g(x, y) and t = h(x, y), and you wish to compute via Fourier optics the convolution(b) Suppose you wish to convolve a large number of different pairs of 1-dimensional functions {g1h1}, {g2h2}, . . . simultaneously; that is,
In a transmission electron microscope, electrons, behaving as waves, are prepared in near-plane-wave quantum wave-packet states with transverse sizes large compared to the object (“sample”) being imaged. The sample, placed in the source plane of Fig. 8.15, is sufficiently thin—with a
Use the convolution theorem to carry out the calculation of the Fraunhofer diffraction pattern from the grating shown in Fig. 8.6.Fig. 8.6 நளாறா ft) Hg(x) -Na 444 transparent 2a m --İ1 சீ = www anbudo /(ka)=k/(2a) | | |···> (b) 4n/(ka)
Sketch the Fraunhofer diffraction pattern you would expect to see from a diffraction grating made from three groups of parallel lines aligned at angles of 120° to one another (Fig. 8.7).Fig. 8.7.
(a) Use an amplitude-and-phase diagram to explain why a zone plate has secondary foci at distances of f/3, f/5, f/7 . . . .(b) An opaque, perfectly circular disk of diameter D is placed perpendicular to an incoming plane wave. Show that, at distances r such that rF ≪ D, the disk casts a rather
Derive a formula for the energy-flux diffraction pattern F(x) of a slit with width a, as a function of distance x from the center of the slit, in terms of Fresnel integrals. Plot your formula for various distances z from the slit’s plane (i.e., for various valuesand compare with Fig. 8.4.Fig.
Conceive and carry out an experiment using light diffraction to measure the thickness of a hair from your head, accurate to within a factor of ∼2.
Consider the scattering of light by an opaque particle with size a >> 1/k. Neglect any scattering via excitation of electrons in the particle. Then the scattering is solely due to diffraction of light around the particle. With the aid of Babinet’s principle, do the following.(a) Explain why
Derive and plot the Airy diffraction pattern [Eq. (8.18)] and show that 84% of the light is contained within the Airy disk. ψ(θ) α Disk with diameter D kᎠᎾ 2 x jinc e-ikxedΣ (8.18)
How closely separated must a pair of Young’s slits be to see strong fringes from the Sun (angular diameter ∼0.5◦) at visual wavelengths? Suppose that this condition is just satisfied, and the slits are 10 μm in width. Roughly how many fringes would you expect to see?
A circularly symmetric light source has an intensity distribution I (α) = I0 exp[−α2/(2α02)], where α is the angular radius measured from the optic axis. Compute the degree of spatial coherence. What is the lateral coherence length? What happens to the degree of spatial coherence and the
An FM radio station has a carrier frequency of 91.3 MHz and transmits heavy metal rock music in frequency-modulated side bands of the carrier. Estimate the coherence length of the radiation.
We developed the theory of real-valued random processes that vary randomly with time t (i.e., that are defined on a 1-dimensional space in which t is a coordinate). Here we generalize a few elements of that theory to a complex-valued random process Φ(x) defined on a (Euclidean) space with n
The longest radio-telescope separation available in 2016 is that between telescopes on Earth’s surface and a 10-m diameter radio telescope in the Russian RadioAstron satellite, which was launched into a highly elliptical orbit around Earth in summer 2011, with perigee ∼10,000 km (1.6 Earth
We have defined the degree of coherence γ12(a, τ) for two points in the radiation field separated laterally by a distance a and longitudinally by a time τ. Under what conditions will this be given by the product of the spatial and temporal degrees of coherence? Y₁2(a, T) = y₁(a)y||
An example of a Michelson interferometer is the Far Infrared Absolute Spectrophotometer (FIRAS) carried by the Cosmic Background Explorer satellite (COBE). COBE studied the spectrum and anisotropies of the cosmic microwave background radiation (CMB) that emerged from the very early, hot phase of
Modern mirrors, etalons, beam splitters, and other optical devices are generally made of glass or fused silica (quartz) and have dielectric coatings on their surfaces. The coatings consist of alternating layers of materials with different dielectric constants, so the index of refraction n varies
Consider monochromatic electromagnetic waves that propagate from a medium with index of refraction n1 into a medium with index of refraction n2. Let z be a Cartesian coordinate perpendicular to the planar interface between the media.(a) From the Helmholtz equation [−ω2 + (c2/n2)∇2]ψ = 0, show
Study the step-by-step buildup of the field inside an etalon and the etalon’s transmitted field, when the input field is suddenly turned on. More specifically, carry out the following steps.(a) When the wave first turns on, the transmitted field inside the etalon, at point A of Fig. 9.7, is ψa =
Show that the PDH method for locking a laser’s frequency to an optical cavity works for modulations faster than the cavity’s response time,and even work for Ω »1/τresponse.More specifically, show that the reflected power still contains the information needed for feedback to the laser. Ω 2
When a thin layer of oil lies on top of water, one sometimes sees beautiful, multicolored, irregular bands of light reflecting off the oil layer. Explain qualitatively what causes this.
A common technique used to reduce the reflection at the surface of a lens is to coat it with a quarter wavelength of material with refractive index equal to the geometric mean of the refractive indices of air and glass.(a) Show that this does indeed lead to perfect transmission of normally incident
(a) Use the Helmholtz-Kirchhoff integral (8.4) or (8.6) to compute all four pieces of the holographically reconstructed wave field. Show that the piece generated byis the same (aside from overall amplitude) as the fieldthat would have resulted if when making the hologram (Fig. 10.6), the mirror
Simplify the analysis by treating each Gaussian light beam as though it were a plane wave. The answers for the phase shifts will be the same as for a true Gaussian beam, because on the optic axis, the Gaussian beam’s phase [Eq. (8.40a) with ω̅ = 0] is the same as that of a plane wave, except
How would you record a hologram if you want to read it out via reflection? Draw diagrams illustrating this, similar to Figs. 10.6 and 10.8.Figure 10.6Figure 10.8. illuminating monochromatic light mirror object Hi mirror wave: Meik(zoos -y sin 6) object wave: O(x, y, z)e*z photographic plate A
A holographic lens, like any other hologram, can be described by its transmissivity t(x, y).(a) What t(x, y) will take a reference wave, impinging from the θo direction (as in Fig. 10.8) and produce from it a primary object wave that converges on the spot (x, y, z) = (0, 0, d)?(b) Draw a contour
By expressing the field as either a Fourier sum or a Fourier integral complete the argument that leads to Eq. (9.58). W(t) W (t +T)= K²Y(t)¥*(t) × V(t + t)¥*(t +T) + K²V (1)V*(1 +t) × ¥*(t)¥(t+t) = W²[1 + |y|| (t)|²] (9.58)
Is it possible to construct an intensity interferometer (i.e., a number-flux interferometer) to measure the coherence properties of a beam of electrons? What qualitative differences do you expect there to be from a photon-intensity interferometer? What do you expect Eq. (9.59) to become? SW (t)8W
A Sagnac interferometer is a rudimentary version of a laser gyroscope for measuring rotation with respect to an inertial frame. The optical configuration is shown in Fig. 9.12. Light from a laser L is split by a beam splitter B and travels both clockwise and counterclockwise around the optical
Derive the factor 1+ (f/fo)2 by which the spectral density of the shot noise is increased at frequencies fz fo
Information on CDs, DVDs, and BDs (compact, digital video, and blu-ray disks) is recorded and read out using holographic lenses, but it is not stored holographically. Rather, it is stored in a linear binary code consisting of pits and no-pits (for 0 and 1) along a narrow spiraling track. In each
A device much ballyhooed in the United States during the presidency of Ronald Reagan, but thankfully never fully deployed, was a futuristic, superpowerful X-ray laser pumped by a nuclear explosion. As part of Reagan’s Strategic Defense Initiative (“StarWars”), this laser was supposed to shoot
Fill in the details of the derivation of all the equations in the section describing the optical frequency comb.
Derive the evolution equations (10.48) for three-wave mixing. You could proceed as follows.(a) Insert expressions (10.27) and (10.28) into the general wave equation (10.30) and extract the portions with frequency ω3 = ω1 + ω2, thereby obtaining the generalization of Eq. (10.33):(b) Explain why
Consider a wave propagating through a dielectric medium that is anisotropic, but not necessarily—for the moment—axisymmetric. Let the wave be sufficiently weak that nonlinear effects are unimportant. Then the nonlinear wave equation (10.22a) takes the linear form(a) Specialize to a
A child, standing in a swing, bends her knees and then straightens them twice per swing period, making the distance ℓ from the swing’s support to her center of mass oscillate asis the swing’s mean angular frequency.(a) Show that the swing’s angular displacement from vertical, θ, obeys the
Consider the secondary wave generated bythe holographic reconstruction process of Fig. 10.8, Eq. (10.7), and Ex. 10.2.(a) Assume, for simplicity, that the mirror and reference waves propagate nearly perpendicular to the hologram, so θo « 90◦ and θs ≈ 2θo « 90◦; but assume that θs is
Green laser pointers, popular in 2016, have the structure shown in Fig. 10.13. A battery-driven infrared diode laser puts out 808-nm light that pumps aNd:YVO4 laser crystal (neodymium-doped yttrium vanadate; a relative of Nd: YAG). The 1,064-nm light beam from this Nd:YVO4 laser is frequency
Derive the solution (10.54) to the evolution equations (10.47) for frequency doubling, and verify that it has the claimed properties. d'Az ik dz 2 = (A₁)², d'A₁ dz =ik AzA; K=B₁, 200703 €0c³n²n3 -dijk fi(¹) f(¹) f(3) (10.47)
Explain why the nonlinear susceptibilities for an isotropic medium have the forms given in Eq. (10.25).What are the corresponding forms, in an isotropic medium, of χij klmn and χijklmnp? Xij = Xogij, Xijkl = dijk = 0, X4(gij9kl + gik9jl +9ilgjk), Xijklm = 0,.... (10.25)
Derive Eqs. (10.34b) and (10.34c) for the amplitudes of waves 1 and 2 produced by three-wave mixing. dA(¹) dz dA (²) dz = i^/ / dijk(³) A(?) at w₁ = 03 — @₂, k₁ = k3 — k₂i jkAA(2)* = ikdijkA@40* (3) (1)* - at @₂ = @3@₁, K₂=k3 - k₁. (10.34b) (10.34c)
Estimate the magnitude of the e-folding length for an optical parametric amplifier that is based on a strong three-wave nonlinearity.
A homogeneous, isotropic, elastic solid is in equilibrium under (uniform) gravity and applied surface stresses. Use Eq. (11.30) to show that the displacement inside it, ξ(x), is biharmonic, i.e., it satisfies the differential equationShow also that the expansion Θ satisfies the Laplace
A microcantilever, fabricated from a single crystal of silicon, is being used to test the inverse square law of gravity on micron scales (Weld et al., 2008). It is clamped horizontally at one end, and its horizontal length is ℓ = 300 μm, its horizontal width is w = 12 μm, and its vertical
Showing 300 - 400
of 512
1
2
3
4
5
6
Step by Step Answers
Get 50% OFF
Claim Now
